On April 24, we released Snowflake Arctic with a key goal in mind: to be truly open. In line with that goal, the Snowflake AI Research team is writing a series of cookbooks to describe how to pretrain, fine-tune, evaluate, and serve large-scale mixture-of-experts (MoEs) such as Arctic. We will share our journey of training the Arctic model, our findings related to sourcing and composing pre-training data, designing MoE architectures, co-designing models with training and inference systems in mind, and methods for instruction-tuning and evaluating the models.
For the full series, please go to the Snowflake Arctic cookbook catalog.
The past few months have been filled with a dizzying array of open source LLMs and innovative ways to fine-tune and serve them, making these models more and more accessible. Despite this buzz, relatively little around the idiosyncrasies of training MoE models has been shared with the public. In this blog post, we will (1) provide an overview of instruction-tuning, (2) discuss our model’s abilities, (3) give a breakdown of our fine-tuning dataset mix, and (4) discuss a few solutions to some of the problems we ran into when fine-tuning a such a sparse model with a large number of experts.
Why instruction-tuning?
The goal of instruction-tuning is to teach an LLM that has already acquired basic language skills during pre-training how to accurately follow instructions and perform a wide variety of textual tasks. Typically, instruction-tuned models go through one or two stages:
- Supervised fine-tuning (SFT) on a mixture of prompt-completion style datasets covering various use cases related to general instruction following and reasoning. If there is a narrower focus, general SFT can be followed by another round of SFT focused on more specialized use cases, such as chat or code generation only, to further boost the performance in those areas.
- Optionally, alignment training using preference data with algorithms like PPO and DPO.
We adopted a more straightforward approach to fine-tuning and relied on a mixture of general instruction-following tasks, code, math, and chat data prepared with the requirements of LLMs‘ enterprise applications in mind. Although Arctic-Instruct can engage in multi-turn conversation, it is not explicitly optimized for such a setup.
Arctic-Instruct performance
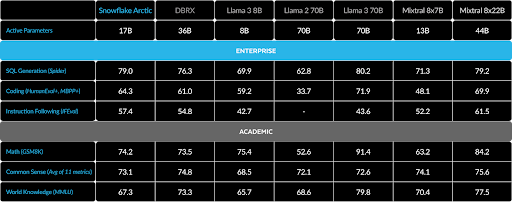
As covered in the launch blog, Arctic-Instruct performs well on most non-generative and academic benchmarks, and excels at enterprise-specific tasks. Arctic-Instruct’s average performance across enterprise benchmarks outperforms DBRX, Mixtral 8x7B, Llama 2 70B, and comes within striking distance of Llama 3 70B and Mixtral 8x22B, which are likely trained on a lot more compute (e.g., Llama 3 70B is pretrained on 16x more compute than Arctic). Our model also performs competitively on the general commonsense reasoning benchmarks.
Arctic-Instruct does have conversational capabilities, but is optimized for single-turn interactions. Furthermore, we have not performed RLHF/DPO or any alignment training whatsoever. We invite the community to do so and are going to release tools to make it easy to run fine-tuning on the model. Even without any preference training, Arctic-Instruct achieves a score of 7.95 on MTBench, with a turn-1 score of 8.31, and performs competitively on the Helpful, Honest, & Harmless (HHH) alignment dataset.
The dataset
We fine-tuned Arctic on a diverse dataset with approximately 1.4M examples consisting of 800M tokens. We deduped this data using Minhash-deduplication with a similarity threshold of 0.7.
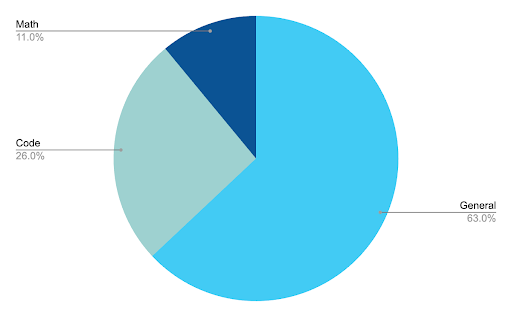
Here’s a more detailed breakdown of our dataset:
- General: This portion of our dataset consists of diverse instruction-response pairs, with and without chain-of-thought (CoT) reasoning, in zero and few-shot setups.
- Code: The coding split consists of programming problems and conceptual questions on programming topics. It is heavily weighted towards the most popular languages on GitHub, with over 50% of the examples in Python and a significant minority in Java, JavaScript, and Go.
- Math: Most of this data is in the form of word problems with explanation traces. These problems are solvable with arithmetic and simple algebra, e.g., the ability to solve linear equations.
- Identity questions: These are 1k examples used to train the model to correctly respond with its name, how it was trained, etc. We generated these examples in two different ways. Some were derived from templates and others were obtained by first manually labeling a seed set and then generating paraphrases of these.
Ablations
Because of this model’s size, we performed ablation experiments to finalize the dataset mix in two stages:
- We performed a larger number of experiments focusing on the proportions of chat, math, and programming data on smaller MoE models (first 2B active parameters, and then 7B active parameters) that we pretrained. The result of this stage was a few dataset candidate “beams.”
- We followed this up with a smaller round of experimentation on the larger model (17B active parameters), starting with these candidates to converge to the final dataset collection.
Some interesting things we observed are:
- At the smaller model size, more math data translated to better scores on programming benchmarks in addition to math. This code improvement evaporated at the larger model size, probably owing to the very strong coding capabilities of our base model.
- At both model sizes, we observed much better results on math benchmarks when we combined our math datasets with the rest of the mix (coding, chat, etc.) than when we fine-tuned on it alone. This suggests that our models quickly overfit to the reasoning patterns in our math dataset if exposed to those alone.
The fine-tuning process
Hyperparameters
We full-parameter fine-tuned our model for two epochs using a learning rate of 2e-5, with the learning rate warm-up over the first 5% of training steps followed by cosine decay. Training was done on 32 nodes (256 H100 GPUs) with expert parallelism and ZeRO-2. We employed a per-device batch size of 1 with a global batch size of 256 sequence-packed examples. We used the standard cross-entropy loss function applied only to the completion tokens in each example.
Challenges and solutions of fine-tuning MoE models
Throughout our journey in instruction-tuning Arctic, we discovered several challenges unique to the training large MoE models. In this section, we present several of the problems we faced and how we attempted to overcome them.
Problem No. 1: Expert stability. One challenge arises from our very sparse MoE architecture itself with 128 experts. For each fine-tuning example, each token in the minibatch is routed to two experts. However in the median case, since the number of completion tokens is a few hundred at the most, each expert will see < 1 tokens per example. As a result of this sparsity, the training of experts can become unstable.
Problem No. 2: Training efficiency. The Arctic-Instruct model has 480B parameters, and instruction-tuning can take several thousand GPU-hours. The naive approach to fine-tuning can have several inefficiencies. In particular, our training system is most efficient if we fine-tune with all examples padded to the same length (in our case 4096). This means a significant amount of compute can be wasted on the padding, which does not contribute to actual training progress.
Notably, both of these challenges are fine tuning specific because for pre-training you train on all tokens and it is trivial to pack sequences to maximum length without any padding. Consequently, we borrowed an idea from pretraining.
Solution No. 1: Packing multiple examples into a single sequence. A standard practice from pre-training, which we repurposed in instruction-tuning, is sequence packing. Instead of just a single (prompt, completion) pair in each sequence of length 4096, we “packed” multiple examples into each sequence in the form (prompt_1, completion_1, …, prompt_n, completion_n). Sequence packing ensures more examples fit into each batch and thus improves training throughput.
Solution No. 2: Packing conversation turns into a single example. The simplest way to train on multi-turn examples is to unroll them, with a separate training point for each assistant completion. Instead, we treat each conversation as a single training example and jointly train on all assistant completions. This not only reduces the training compute required per conversation but also helps to alleviate the expert gradient sparsity issue by increasing the fraction of trainable tokens in each batch.

Solution No. 3: Freezing MoE layers during training. Another solution we tried to improve training efficiency is to freeze all MoE layers during training. This is an efficiency technique that is specifically tailored to our model architecture (because of the residual dense layer in arctic) and is likely more suited for our architecture than plain LoRA. This drastically reduces the compute and size of gradients during training, allowing it to be done on much fewer GPUs. We observed that this didn’t degrade general non-generative benchmarks + GSM8K. However, some other generative benchmarks like HumanEval were significantly affected and dropped by 5-6 points. Though we did not use it for the final recipe, it was an approximation we found helpful when iterating over different data compositions.
Load balancing
Another important consideration when training MoE models is how evenly tokens are routed across the experts. Most MoE architectures define a fixed token capacity for each expert in a layer to minimize the computational load on any single expert. If the routing function for an MoE layer assigns too many tokens to an expert, the excess tokens are dropped and are simply passed to the next layer via residual. Thus, it is critical that the model learns to load balance as well as possible. In the early phases of our fine-tuning, we were quite paranoid about this because of the small effective training tokens we use during fine-tuning than in pre-training.
Throughout the fine-tuning process, we ensured that token routing was indeed close to uniform by monitoring the MoE load balancing loss and ensuring that it stayed close to the theoretical minimum. More specifically, we employed a normalized variant of the GShard expert loss, which is defined per layer to be

where k is a constant (0.01), E is the number of experts, S is the number of tokens in the batch, c_e is the number of tokens that are routed to expert e, and m_e is the mean gating weight assigned to expert e across all S tokens. This loss function is minimized when the routing function assigns a gating weight of 1/E to every expert for every token. In that case, the mean gating weight is 1/E, and each expert is assigned around S/E tokens, so

Since this loss is summed over the 35 transformer layers in our model, the minimum possible value for this loss is 0.35. We observed that, throughout fine-tuning our balance loss hovered around 0.35, signifying that our model nearly perfectly balances input tokens across its experts!
Conclusion
We have instruction-tuned our Arctic base model to perform well on general textual tasks and excel at enterprise-related ones, like SQL and coding. We will continue to share more of our findings on instruction-tuning and look forward to working with the open-source community to make powerful LLMs more accessible to the public. Stay tuned as more updates will continue to drop in the Snowflake Arctic cookbook catalog.
